大津算法（OTSU）
- 算法思想
  - 目标
  - 灰度直方图
  - 聚类
  - 步骤
- 算法
- 代码实现
  - C语言实现

大津算法（OTSU）

在图像处理领域，我们会遇到如下需求：把图像中的目标物体和背景分开。比如背景用白色表示，目标物体用黑色表示。此时我们知道目标物体的灰度值相互接近，背景灰度值相互接近，那么用大津算法能很好把目标从背景当中区分开来。

算法思想

目标

比如对于下面这张灰度图片 origin 目标物体是中间黑色的几何物体，我们想让这些物体和背景区分更明显一些，比如让物体为纯黑，背景全白。那么我们就需要找到一个合适的阈值，使图片上灰度值大于这个阈值的像素点为255（白色），灰度值小于阈值的像素点为0（黑色）。也就是变成下面这幅图： output 那么大津算法需要处理的就是找到最佳的阈值，让目标和物体尽可能分离开。

灰度直方图

为了找到合适的阈值，我们首先观察原图的灰度直方图📊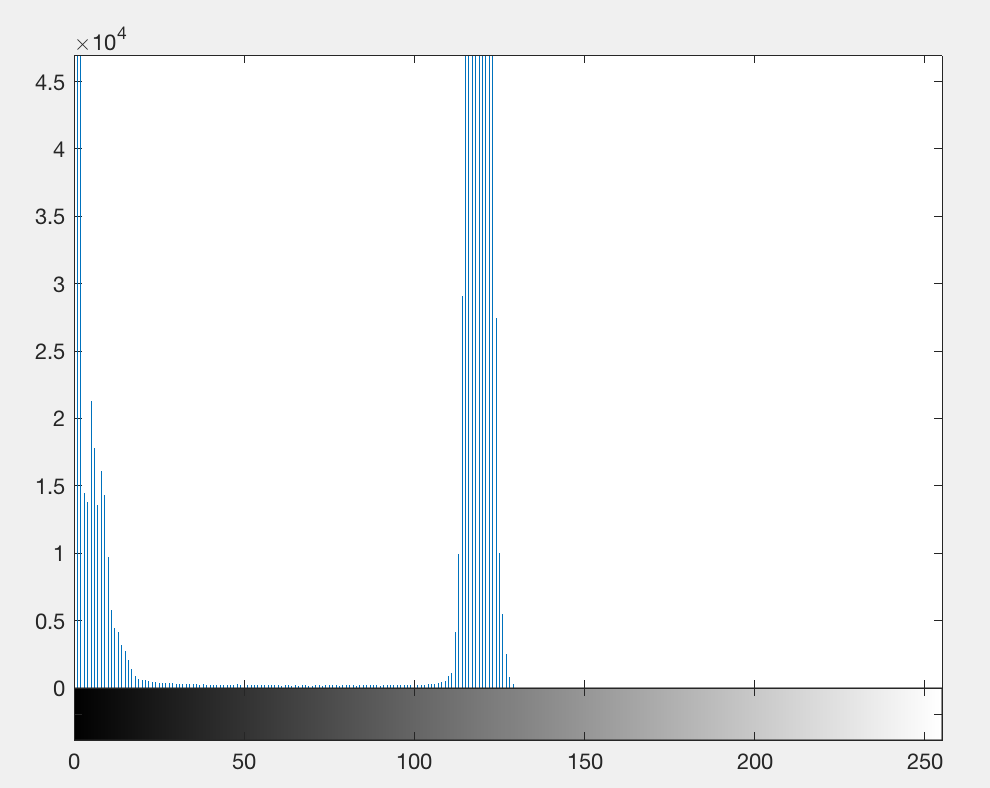： histogram 这是用 Matlab 对原图形成的灰度直方图，灰度直方图的含义是统计图像中不同灰度值的分布情况。由图我们可以看出两个尖峰，在灰度值为0～20的地方存在一个尖峰，代表原图中有大量像素点灰度值为0～20，经观察我们可以认为这部分对应于目标物体。同理我们可以看出背景的灰度值大多集中于100～140之间，为了让目标和背景区分更加明显，我们想让目标物体的灰度值全为0，背景的灰度值全为255，这种处理手法也称为二值化法。

那么阈值取多少合适呢？从图上看似乎取50～100中的任意一点都可以，但是实际情况并不想参考图那样明显，有些图片背景和目标物体较为接近，我们需要一个算法来找到最优阈值才行。

聚类

首先我们思考什么样的东西才能成为一类，而我们又是怎么分类的。对于参考图来说，我们可以认为灰度值接近的为一类，灰度值不接近的不是同一类。那我们又是如何衡量灰度值接近的程度呢？这里面就需要用到方差的概念。方差相比大家都了解，同一类的物体方差小，不同类的物体方差大。所以对于此图我们希望分类的结果是对于灰度值相近的同一类物体，它的方差最小，称为类内方差最小。灰度值不接近的不同类物体，它的方差大，称为类间方差最大。

步骤

所以步骤总结如下：首先我们要形成参考图的灰度直方图，这样方便我们找到最佳阈值。接下来我们通过穷举每一个灰度值，计算以此为阈值的类内和类间方差。找到能形成类内方差最小的或类间方差最大的阈值，这个就是我们要找的最佳阈值。

算法

下面以两类分割讲解下具体的算法，实际上大津算法可以分割多类出来。

我们定义$\delta_i^2 $为第 i 类的类内方差，$\delta_w^2 $为类内方差和，$\delta_b^2 $为类间方差和；$\omega_i$为第 i 类的概率分布，t 为当前假设的阈值，p(i) 为灰度值为 i 的概率密度。则对于 2 类问题： $\omega_1(t)=\sum_0^t p(i) \\ \delta_w^2(t)= \sum _{i=1}^{i=2}\omega_i(t)\delta_i^2$ 而最小化类内方差和最大化类间方差是相同的，即 $\delta_b^2(t)=\delta^2-\delta_w^2=\omega_1(t)\omega_2(t)[\mu_1(t)-\mu_2(t)]^2$ 类均值$\mu_1(t)$： $\mu_1(t)=[\sum_0^t p(i)*i]/\omega_1$

遍历 t 所有的可能值，找到最小$\delta_w^2$或最大$\delta_b^2$所对应的 t 值，就是我们的最佳阈值。

代码实现

C语言实现

/* OTSU 算法
 * *src 存储灰度图像，width 图像宽，height 图像长
 * 返回最佳阈值
 */
int otsu(const int *src, int width, int height)
{
    int histogram[256]; //存储灰度直方图，这里为256色灰度
    int t,thred;
    float wf,wb,ub,uf,curVal,maxVal;
    int sumb=0,sumf=0,sumW=0,sumPixel=width*height;
    wb=wf=maxVal=0.0f;
    
    //求灰度直方图
    memset(histogram,0,sizeof(histogram));
    for(i=0;i<width*height;i++)
    {
        histogram[src[i]]++;
    }
    
    for (i=0;i<256;i++)
        sumW+=i*histogram[i];
    
    //枚举每个灰度    
    for(t=0;t<256;t++)
    {
        //求两类类概率密度
        wb+=histogram[t];
        wf=sumPixel-wb;
        if (wb==0||wf==0)
            continue;
        
        //求类均值
        sumb+=i*histogram[t];
        sumf=sumW-sumb;
        ub=sumb/wb;
        uf=sumf/wf;
        
        //求当前类间方差
        curVal=wb*wf*(ub-uf)*(ub-uf);
        if(curVal>maxVal)
        {
            thred=t;
            maxVal=curVal;
        }
    }
    return thred;
}